Ph.D. Student
Charles University, Prague
Faculty of Mathematics and Physics, Algebra department
supervisors: Tomáš Mikolov, Jiří Tůma
Junior Researcher
Czech Institute of Infromatics, Robotics, and Cybernetics, Prague
team leader: Tomáš Mikolov
RESEARCH INTERESTS
I do research in the field of complex systems. Namely, I am interested in studying complex systems as possible models of artificial evolution where intelligent structures could emerge. As a mathematician, one if my goals is to study the formal notions of complexity and chaos in the context of discrete dynamical systems. In my research so far, I have explored what formal properties of discrete systems correlate with our intuitive understanding of complexity and chaos. I am also interested in the question whether chaotic systems have a nontrivial computational capacity.
Recently Published Papers and Papers in Progress
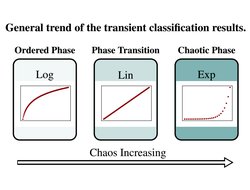
We introduce a novel complexity metric which measures the asymptotic growth of the average computation time in cellular automata (CA). We use it to classify CA dynamics and to automatically search for CA with complex behavior.
Generalization of the previous paper about classifying complex systems. We show the method works across various classes of discrete systems. We show the method indicates a region of systems at a phase transition and demonstrate that many hand-designed complex systems belong to this region.
We study the computational capacity of elementary cellular automata (ECA) by measuring how many other ECA can they emulate. The results suggest that the most chaotic ECA are exactly those that cannot emulate any other. Thus, we propose a new definition of chaos in dynamical systems related to their computing power.
