Abstract
In order to develop systems capable of modeling artificial life, we need to identify which systems can produce complex behavior. We present a novel classification method applicable to any class of deterministic discrete space and time dynamical systems. The method distinguishes between different asymptotic behaviors of a system’s average computation time before entering a loop. When applied to elementary cellular automata, we obtain classification results, which correlate very well with Wolfram’s manual classification. Further, we use it to classify 2D cellular automata to show that our technique can easily be applied to more complex models of computation. We believe this classification method can help to develop systems, in which complex structures emerge.
Informal Summary
In this paper we define a new method of classifying the dynamics of discrete systems; we call it the transient classification. The method is fairly simple and works as follows.
We consider discrete dynamical systems of the form $D = (S, F)$ where $S$ is a finite set of configurations of the system and $F: S \rightarrow S$ is the global update rule. You can image a cellular automaton operating on a finite lattice with periodic boundary conditions or a random Boolean network. As $S$ is finite, for every $u \in S$ the trajectory $u, F(u), F^2(u), \ldots,$ eventually enters a loop. We call the preperiod of the sequence the transient and the looping part the attractor.
We can interpret these notions in the following computational terms: within the transient, information from the initial configuration is processed in an irreversible manner, whereas the loop acts as a memory unit of the system. Therefore, we can interpret the transient length as the computational time of the system (depending on a particular initial configuration).
Our goal is to measure the average computation time of a discrete dynamical system $D=(S, F)$ by measuring its average transient length $T(D)$. We simply do this by randomly sampling initial configurations and using computer simulations to detect the loops and transient lengths. We do this until the variance of the data is “reasonably” small.
Let us consider a sequence of systems operating on configuration spaces of growing size: $$D_1 = (S_1, F_1), D_2 = (S_2, F_2), D_3 = (S_3, F_3), , \ldots$$ That is, $F_i: S_i \rightarrow S_i$ and $|S_i| < |S_{i+1}|$ for each $i$. For instance, each $D_i$ can be a cellular automaton given by a fixed local rule, operating on a finite cyclic grid of growing size.
The key principal of the transient classification is to estimate the average computation time of each system and determine the asymptotic growth of the sequence. This is illustrated in the figure below.

We try to compute the average transient values $T(D_i)$ for $i$ as large as possible before the computation of the value takes too long (we set some reasonable time bound). We then use regression methods to see, whether the data fit to a bounded, logarithmic, linear, polynomial, or an exponential function. If the fit to any of the function is good (i.e., with $R^2$ score above $90 %$) we classify the sequence of systems to one of the classes Bound, Log, Lin, Poly, or Exp.
Surprisingly, many cellular automata exhibit very clear asymptotic growth of their average computation time and the classification seems to work good on them. As an example, we show some figures for elementary automata described by their Wolfram numbers.

The results show that ordered systems generally correspond to Bound or Log classes whereas chaotic systems to the Exp class. We have examined many complex systems such as the Turing complete elementary automaton 110, or Game of Life to find out they all fit to linear functions the best. We therefore formed a hypothesis that complex systems belong to the Lin or Poly classes, which correspond to the “transition region” from logarithmic to exponential behavior. We further used the classification method to automatically search for complex automata in large spaces by searching for automata with linear or polynomial transient growth. Some interesting results are shown below.
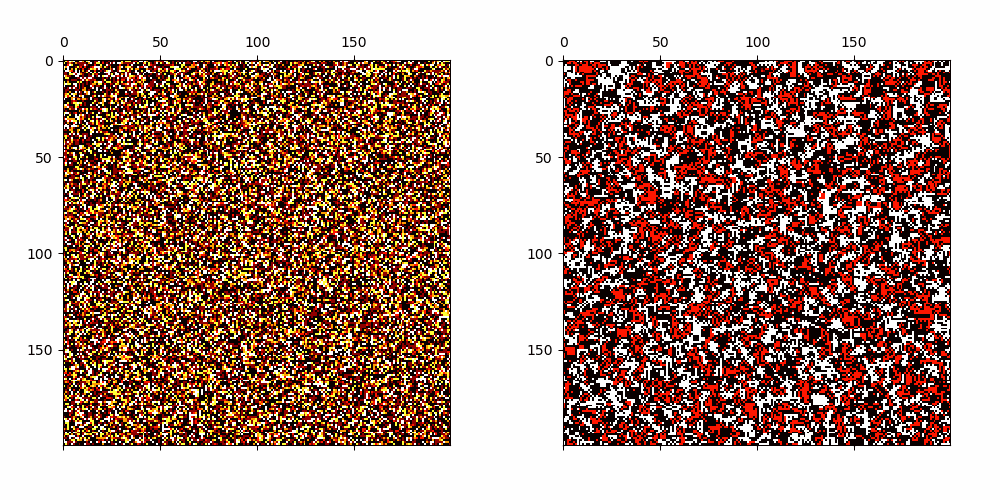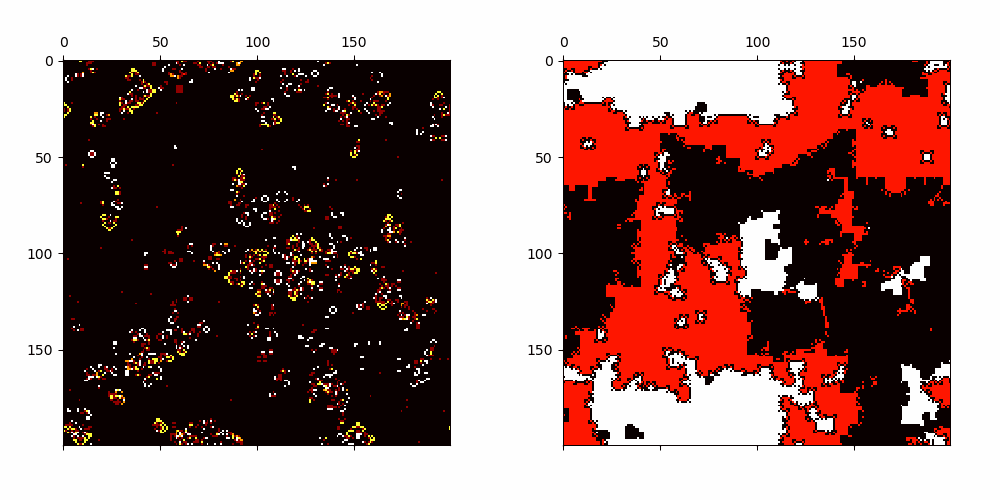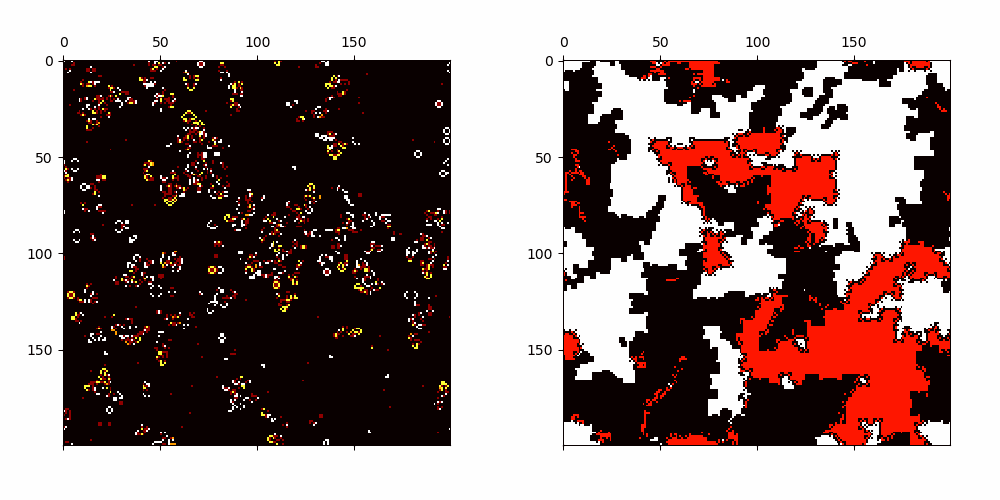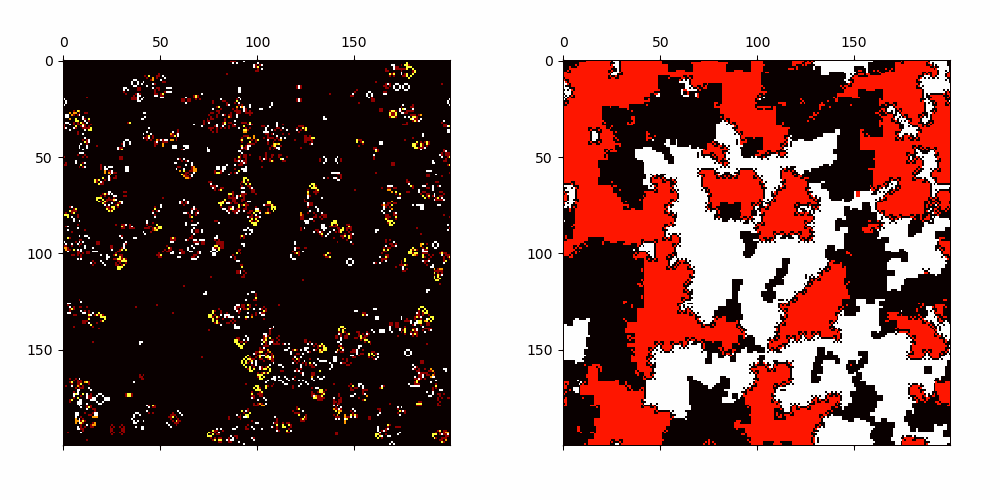
Cellular Automata with emerging patterns which have linearly growing average transients.
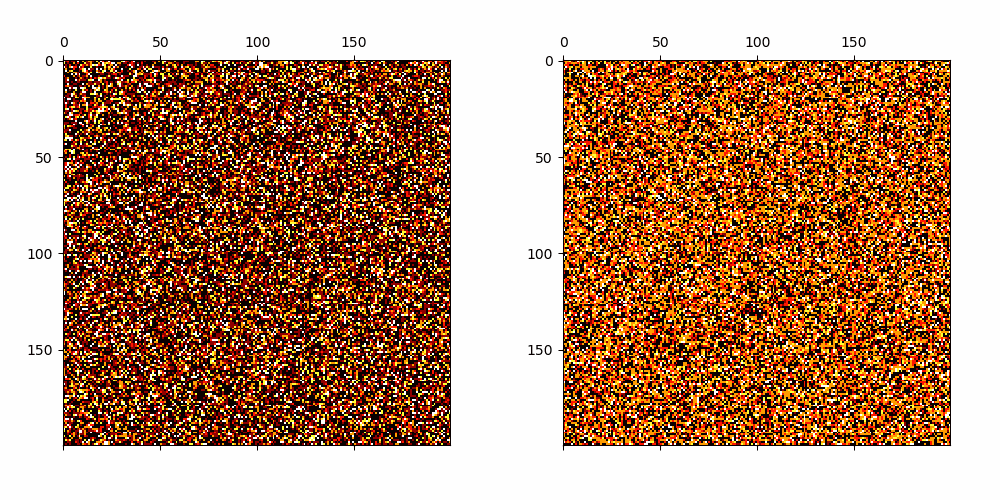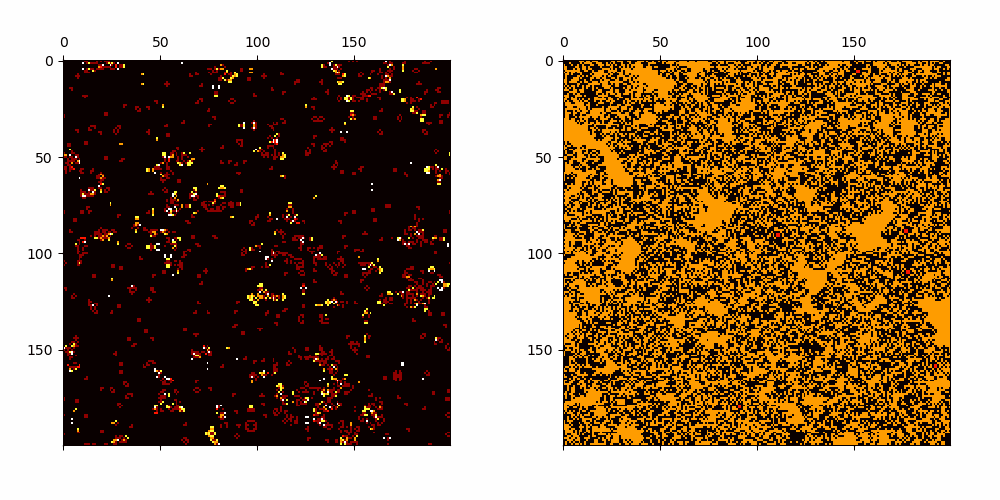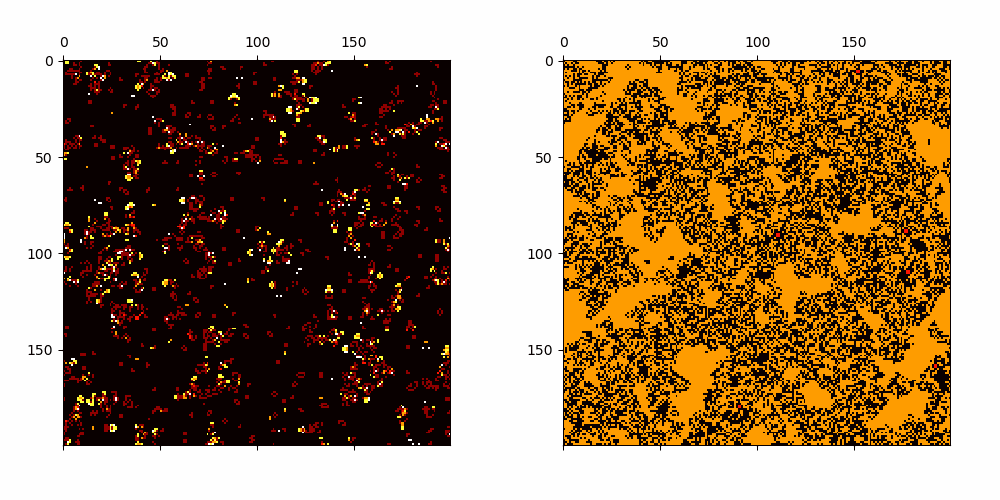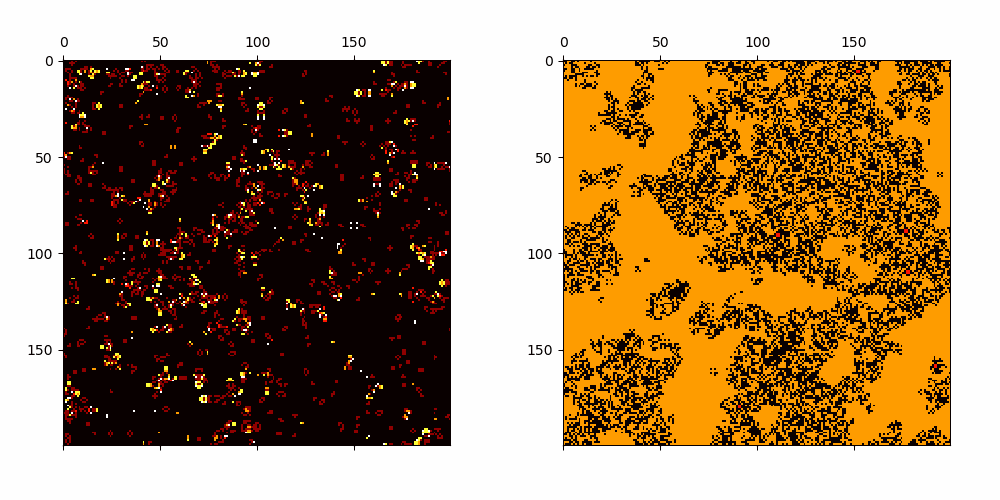
Cellular Automata with emerging patterns which have polynomially growing average transients.
We have applied the transient classification to other discrete dynamical systems to show it works across various systems and presented the results in our subsequent paper, which is now in the review process for the special issue of the ALife journal. The results suggest that there is a general trend across discrete systems which we describe in the paper:
The interesting property of the transient classification is that it was able to qualitatively distinguish the phase transition between order and chaos by identifying it with linear or polynomial transient growth.
We note that our results are experimental and that the asymptotic behavior of systems in the Lin or Poly class might eventually turn out to be logarithmic or exponential. In that case, such systems would exhibit a significantly longer time before they converge to their typical long-term behavior. That, too, is a typical property of systems at a phase transition.