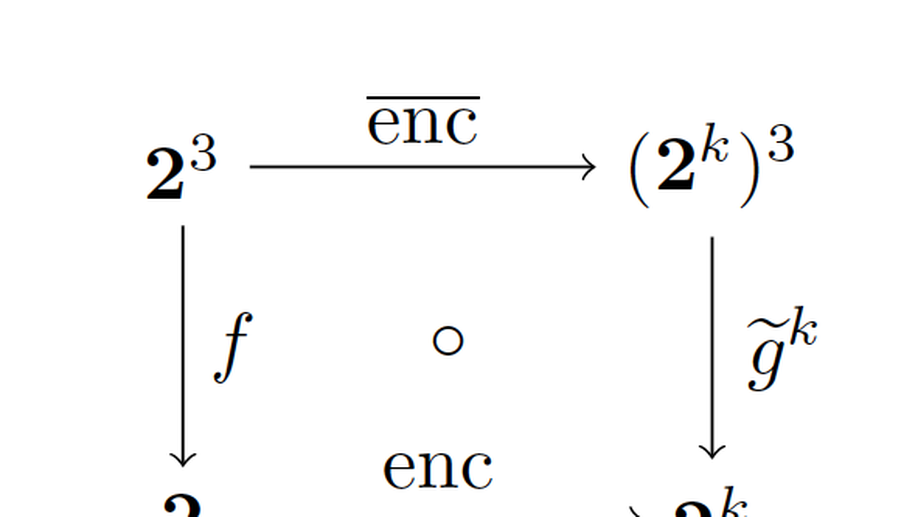
Computational Hierarchy of Elementary Cellular Automata
We study the computational capacity of elementary cellular automata (ECA) by measuring how many other ECA can they emulate. The results suggest that the most chaotic ECA are exactly those that cannot emulate any other. Thus, we propose a new definition of chaos in dynamical systems related to their computing power.
Classification of Discrete Dynamical Systems Based on Transients
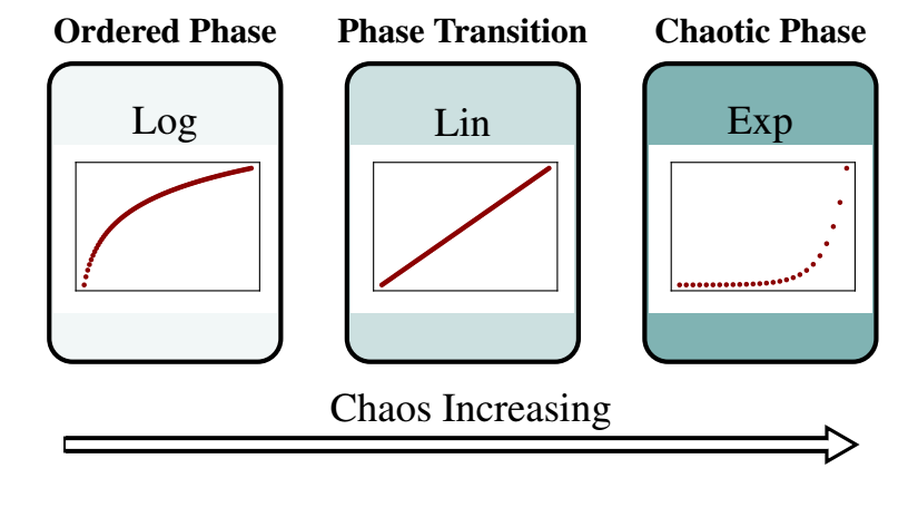
Generalization of the previous paper about classifying complex systems. We show the method works across various classes of discrete systems. We show the method indicates a region of systems at a phase transition and demonstrate that many hand-designed complex systems belong to this region.

Classification of Complex Systems Based on Transients
We introduce a novel complexity metric which measures the asymptotic growth of the average computation time in cellular automata (CA). We use it to classify CA dynamics and to automatically search for CA with complex behavior.