
Self-Replication and Computational Universality
We study the relationship between self-replication and computation in dynamical systems. We challenge a long-standing hypothesis that Turing completeness is a sufficient condition of self-replication. Concretely, we clarify what computational universality means for physical systems and construct a cellular automaton that is Turing-universal but cannot sustain non-trivial self-replication.
Simulation Limitations of Affine Cellular Automata
We study computational capacity of cellular automata via the notion of intrinsic simulation: We say that automaton A is simulated by B if each space-time diagram of A can be, after suitable transformations, reproduced by B. We formalize intrinsic simulation in algebraic terms and show how this framework enables deeper algebraic tools for proving negative results about CA computational power. Our main result shows that (almost) every affine/abelian/linear CA is very limited in terms of what it can simulate
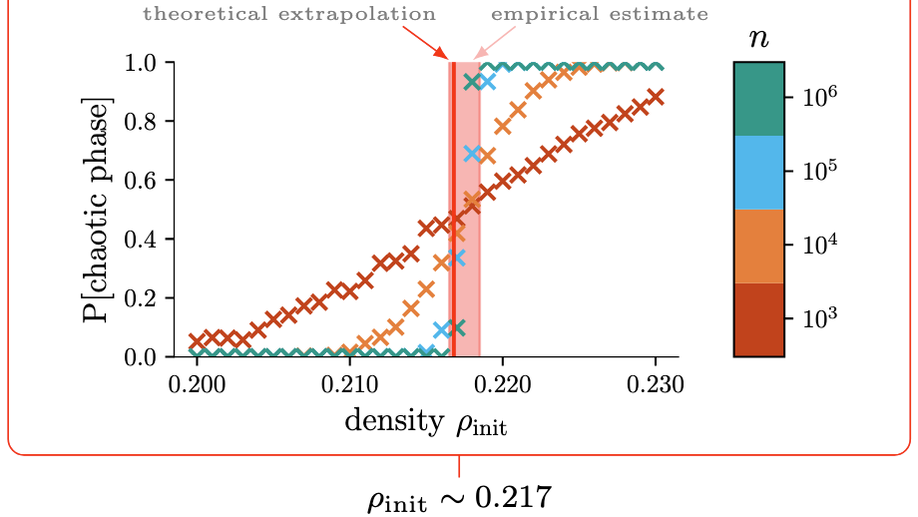
Dynamical Phase Transitions in Graph Cellular Automata
We relax the cellular automata regular grid structure to random graphs, obtaining graph cellular automata, and use the dynamical cavity method (and its backtracking variant) to derive asymptotically exact results for their dynamics on sparse random graphs. We focus on rules inspired by opinion formation and for varying initial biases, we find sharp dynamical phase transitions that determine convergence speed and the resulting attractors—clarifying when systems reach consensus or sustain long-term coexistence of two opinions.
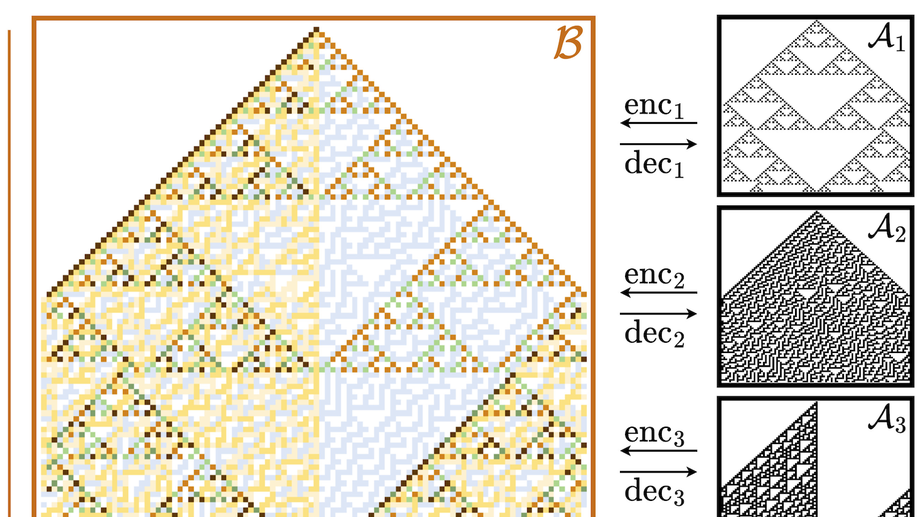
Studying Encoder–Decoder Relation Between Cellular Automata to Uncover Their Computational Structure
We study the computational capacity of CAs via the encoder-decoder relation: a stronger variant of intrinsic simulation. We propose a method to efficiently search for such relations between two given automata. We demonstrate the results on the class of elementary CAs, presenting a rich hierarchy of their relationships, showing that the number of elementary automata with unique dynamics can be reduced from 88 to 52. Further, we show that some automata thought as unique have in fact equivalent computational capacity. We believe that using similar approaches, the number of unique automata can be dramatically reduced in the future.
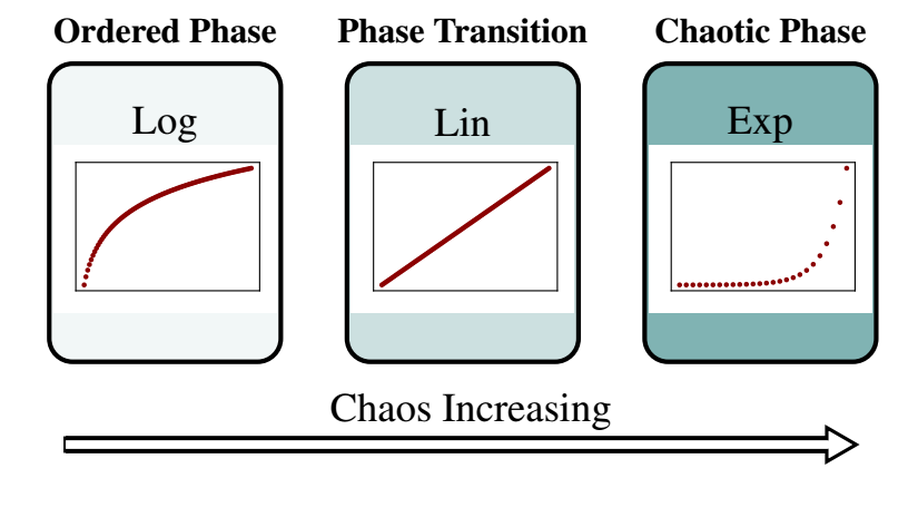
Classification of Discrete Dynamical Systems Based on Transients
We introduce a novel complexity metric which measures the asymptotic growth of the average computation time in discrete dynamical systems. We use it to classify cellular automata, Turing machines, and random Boolean networks and to automatically search for systems with complex behavior.